前言

最近开发需要处理利用贝塞尔曲线解决平滑的动效,读了一篇Catmull-Rom的论文,记录一下这篇文章.

Interpolating Points in iOS with UIBezierPath

最近，我一直在开发一个移动应用，其中包含一个可视化组件，该组件由平滑曲线组成，这些曲线穿过任意的、变化的二维点集。在 iOS 中实现这一功能最直接的方法是使用由 UIBezierPath 定义的平滑曲线序列，但开发人员需要以这样一种方式构造路径中的三次贝塞尔曲线：它们是平滑的并且恰好通过数据点。

在这篇文章中，我将描述两种简单且常用的方法，用于使用三次贝塞尔曲线插值点（不会深入探讨它们背后的数学原理），并链接到我编写的包含这两种插值方法实现的 git 仓库。

UIBezierPath 和贝塞尔曲线

在 iOS 中，我们使用 UIBezierPath 绘制直线段和曲线段。通过 addLineToPoint: 添加线性段非常简单，但如何绘制曲线形状呢？

可以通过在路径中添加三次贝塞尔曲线来绘制曲线段。三次贝塞尔曲线由四个控制点定义——这四个点的位置定义了曲线的形状。在下图中，每个点都是欧几里得空间中的 2D (x,y) 点。

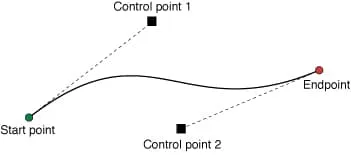
向 UIBezierPath 添加贝塞尔曲线很简单：

1
2
3
4

UIBezierPath* bezierPath = [UIBezierPath bezierPath];
[bezierPath moveToPoint: CGPointMake(77.5, 36.5)];
[bezierPath addCurveToPoint: CGPointMake(101.5, 72.5) controlPoint1: CGPointMake(67.78, 56.83) controlPoint2: CGPointMake(75.76, 76.01)];
[bezierPath addCurveToPoint: CGPointMake(157.5, 66.5) controlPoint1: CGPointMake(127.24, 68.99) controlPoint2: CGPointMake(127.69, 97.13)];

在上面的代码中，UIBezierPath 从 (77.5, 36.5) 开始，并使用 addCurveToPoint:controlPoint1:controlPoint2 添加了两条三次贝塞尔曲线。这两条曲线的样子如下：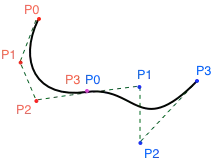

我已经用红色标记了第一条曲线 (C1) 的四个控制点，用蓝色标记了第二条曲线 (C2) 的四个控制点。两条曲线共享一个控制点（C1 P3 和 C2 P0）。C1 的第一个控制点对应于 UIBezierPath 的起点 P0=(77.5, 36.5)，其第一个控制点 (67.78, 56.83) 对应于 P1，依此类推。

显然，两个曲线端点（P0 和 P3）的简单选择将强制曲线恰好通过两个插值点。因此，对于一组N个点，我们可以创建N-1条曲线，使其通过每个点。为了使相邻两条曲线之间的过渡平滑，相邻的控制点（第一条曲线中的 P2 和第二条曲线中的 P1）必须至少共线，理想情况下我们还希望它们具有相同的长度。如果它们不共线，UIBezierPath 将有尖点。问题是，我们如何定位这些内部控制点？

使用 Hermite 和 Catmull-Rom 样条进行平滑插值

两种最常用的插值曲线是 Hermite 和 Catmull-Rom 样条。这些曲线由插值点集定义，并且都可以很容易地转换为一组分段三次贝塞尔曲线——这意味着给定N个拟合点，我们可以创建N-1条三次贝塞尔曲线的控制点，以匹配 Hermite 或 Catmull-Rom 样条。然后将这些三次贝塞尔曲线添加到 UIBezierPath 中。

插值最简单的方法可能是使用 三次 Hermite 样条。计算 Hermite 曲线对应的三次贝塞尔控制点非常简单（请参阅下面示例项目中链接的代码），但当点不规则分布时，它们会表现出极高曲率的”扭结”和环路等问题：

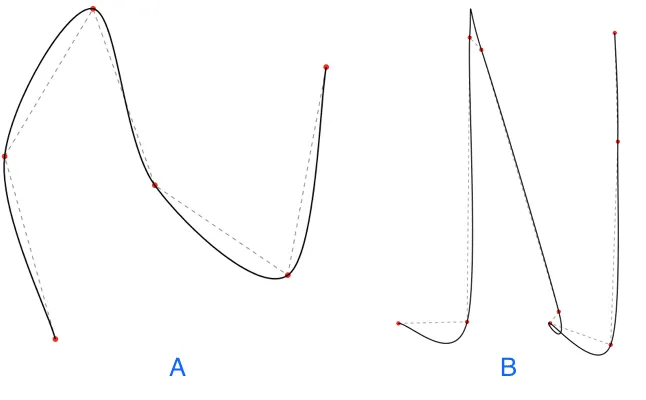
曲线 A 和 B 都是通过 Hermite 插值创建的。曲线 A 看起来很好——点大致均匀分布。然而，曲线 B 由于点的不规则分布而出现扭结和自相交。

另一种用曲线拟合点的选择是使用 Catmull-Rom 样条曲线。与 Hermite 曲线一样，Catmull-Rom 曲线会穿过插值点并生成平滑结果，但它们还提供额外的控制——一个标量 alpha 值（在 0.0 和 1.0 之间），用于控制切线幅度。有关详细信息，请参阅这篇出色的论文，标题为 关于 Catmull-Rom 曲线的参数化，其中讨论了 alpha 的影响。

常用的 alpha 值为 0.0、0.5 和 1.0，分别对应曲线的均匀、向心和弦长参数化。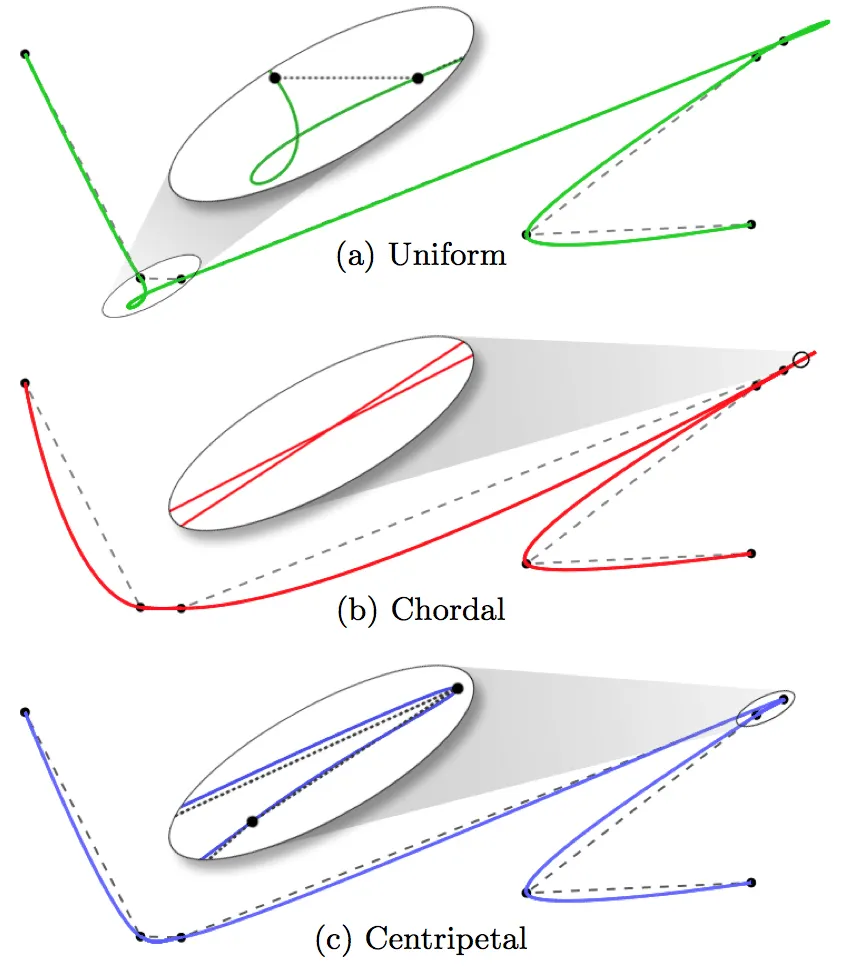

改变 alpha 值对曲线形状有显著影响，尤其是在高曲率区域。需要注意的是，表示 Catmull-Rom 曲线的分段三次贝塞尔曲线在给定插值点Pn处的计算考虑了点Pn-1、Pn、Pn+1 和 Pn+2，因此生成的三次贝塞尔曲线不会穿过第一个和最后一个拟合点。可以添加额外的点，或者将曲线创建为闭合环。

我们可以重新审视之前的曲线 B，看看它作为 alpha=0.5 的 Catmull-Rom 曲线是什么样子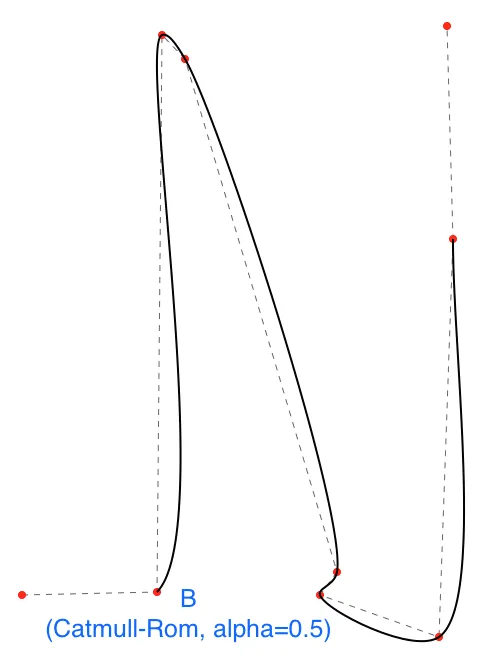： 好多了（但是，请注意它不会穿过第一个和最后一个点）！

代码和示例项目

我创建了一个 UIBezierPath 的分类，UIBezierPath+Interpolation，它添加了使用 Hermite 或 Catmull-Rom 技术用 UIBezierPath 插值点的方法：

1
2
3
4
5
6
7

// pointsAsNSValues 必须是包含 CGPoint 的 NSValue 对象数组。
//
// 示例：
//     const char *encoding = @encode(CGPoint);
//     NSValue *pointAsValue = [NSValue valueWithBytes:&cgPoint objCType:encoding];
+(UIBezierPath *)interpolateCGPointsWithCatmullRom:(NSArray *)pointsAsNSValues closed:(BOOL)closed alpha:(float)alpha;
+(UIBezierPath *)interpolateCGPointsWithHermite:(NSArray *)pointsAsNSValues closed:(BOOL)closed;

这两种方法都可以传递一个标志 closed，用于确定曲线在其端点处是闭合的还是开放的。此外，Catmull-Rom 方法还传递一个介于 0.0 和 1.0 之间的 alpha 值。Hermite 插值方法使用有限差分法计算切线。

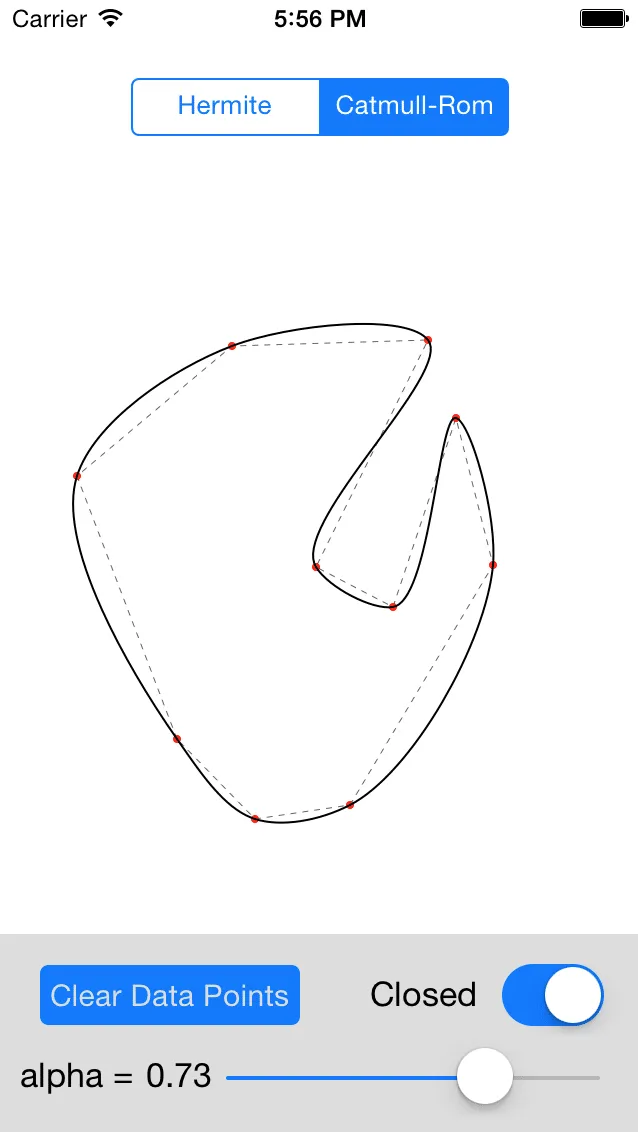
除了分类之外，我还创建了一个小型 iOS 应用程序，它支持添加点并使用任一方法进行拟合，还可以改变 Catmull-Rom 曲线的 alpha 值。该应用程序允许用户动态地调整值并查看其效果。

分类代码和 iOS 应用程序都可以在以下公共 git 存储库中找到：iOS 曲线插值。最终，选择拟合技术更多是艺术而非科学，因为结果的质量通常是主观的。我发现 Catmull-Rom 结果对于大量数据集来说是合理的。